Tīkla teorijā ir ļoti svarīgi izpētīt vai zināt izmaiņu ietekmi impedances robežās vienā no tās atzariem. Tātad tas ietekmēs ķēdes vai tīkla atbilstošās strāvas un spriegumu. Tātad kompensācijas teorēma tiek izmantota, lai zinātu izmaiņas tīklā. Šis tīkla teorēma vienkārši darbojas pēc Oma likuma koncepcijas, kas nosaka, ka ikreiz, kad visā rezistorā tiek piegādāta strāva, pāri rezistoram samazināsies sprieguma daudzums. Tātad šis sprieguma kritums izturēs sprieguma avotu. Tādējādi mēs pievienojam papildu sprieguma avotu apgrieztā polaritātē, kas ir pretstatā sprieguma avotam, un lielums ir līdzvērtīgs sprieguma kritumam. Šajā rakstā ir apskatīts pārskats par a kompensācijas teorēma – darbs ar aplikācijām.
Kas ir kompensācijas teorēma?
Kompensācijas teorēmu tīkla analīzē var definēt kā; tīklā, jebkurā pretestība var aizstāt ar sprieguma avotu, kas ietver nulles iekšējo pretestību un spriegumu, kas līdzvērtīgs sprieguma kritumam pār nomainīto pretestību, jo tajā plūst strāva.
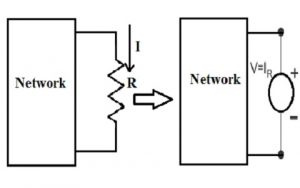
Pieņemsim, ka strāvas 'I' plūsma visā šajā 'R' rezistors & sprieguma kritumi šīs strāvas plūsmas dēļ pāri rezistoram ir (V = I.R). Pamatojoties uz kompensācijas teorēmu, šis rezistors tiek aizstāts ar sprieguma avotu, kas ģenerē spriegumu un tiks vērsts pret tīkla sprieguma virzienu vai strāvas virzienu.
Kompensācijas teorēma Atrisinātie uzdevumi
Tālāk ir doti kompensācijas teorēmas piemēri.
1. piemērs:
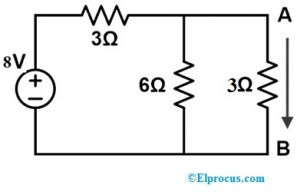
Par šādu ķēdi
1). Atrodiet strāvas plūsmu visā AB atzarā, kad pretestība ir 4Ω.
2). Atrodiet strāvas plūsmu visā AB atzarā ar kompensācijas teorēmu, ja pretestība 3Ω ir mainīta ar 9Ω.
3). Pārbaudiet kompensācijas teorēmu.

Risinājums:
Kā parādīts iepriekš minētajā shēmā, divi rezistori piemēram, 3Ω & 6Ω savienoti paralēli, un arī šī paralēlā kombinācija ir vienkārši virknē savienota ar 3Ω rezistoru, tad būs vienāda pretestība;
Re1 = 6 || 3 + 3 => (6 × 3/6 + 3) + 3
= (18/9) + 3 => 2+3 = 5 Ω.
Balstoties uz Oma likums ;
8 = I (5)
I = 8 ÷ 5
I = 1,6 A
Tagad mums ir jāatrod strāvas plūsma visā AB filiālē. Tādējādi, pamatojoties uz strāvas sadalītāja likumu;
I' = 1,6 (6)/6+3 => 9,6/9 = 1,06 A
2). Tagad mums ir jāmaina 3Ω rezistors ar 9Ω rezistoru. Pamatojoties uz kompensācijas teorēmu, virknē ar 9Ω rezistoru jāiekļauj jauns sprieguma avots un sprieguma avota vērtība ir;
VC = I' ΔZ
kur,
ΔZ = 9 – 3 = 6 Ω & I’ = 1,06 A.
VC = (1,06) x 6 Ω = 6,36 V
VC = 6,36 V
Modificētā shēmas shēma ir parādīta zemāk.
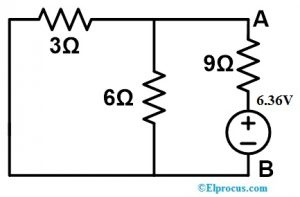
Tagad mums ir jāatrod līdzvērtīga pretestība. Tātad rezistori, piemēram, 3Ω un 6Ω, ir vienkārši savienoti paralēli. Pēc tam šī paralēlā kombinācija tiek vienkārši savienota virknē ar 9Ω rezistoru.
Pieprasīt = 3||6+9
Req = (3×6||3+6) +9
Pieprasīt = (18||9) +9
Pieprasīt = (2) +9
Nepieciešamais = 11 omi
Pamatojoties uz Oma likumu;
V = ΔI x R
6,36 = ΔI (11)
I = 6,36 11
ΔI = 0,578 A
Tādējādi, pamatojoties uz kompensācijas teorēmu; izmaiņas strāvas robežās ir 0,578 A.
3). Tagad mums jāpierāda kompensācijas teorēma, aprēķinot strāvas plūsmu nākamajā ķēdē ar 9Ω rezistoru. Tātad modificētā shēma ir dota zemāk. Šeit tādi rezistori kā 9Ω un 6Ω ir savienoti paralēli, un šī kombinācija ir vienkārši virknē savienota ar 3Ω rezistoru.
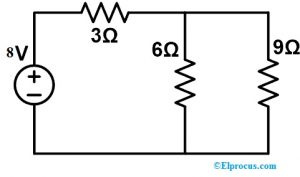
REq = 9 | | 6+3
REq = (6 × 9 | 6 + 9) + 3
REq = (54 | 15) + 3
REq = 45+54/15 => 99/15 => 6,66 omi
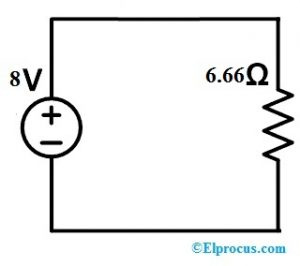
No iepriekš minētās shēmas
8 = I (6,66)
I = 8 ÷ 6,66
I = 1,20A
Pamatojoties uz pašreizējo dalītāja noteikumu;
I'' = 1,20 (6)/6+9
I'' = 1,20 (6)/6+9 => 7,2/15 => 0,48 A
ΔI = es' - es'
ΔI = 1,06-0,48 = 0,578 A
Tāpēc kompensācijas teorēma ir pierādīta, ka izmaiņas strāvā tiek aprēķinātas no teorēmas, kas ir līdzīga strāvas izmaiņām, kas izmērītas no faktiskās ķēdes.
2. piemērs:
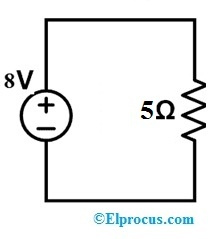
Pretestības vērtība abos sekojošās ķēdes A un B spailēs ir mainīta uz 5 omi, tad kāds ir kompensācijas spriegums?
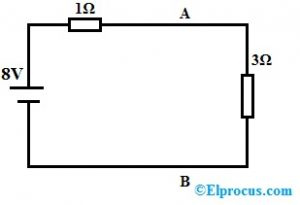
Iepriekš minētajai shēmai, pirmkārt, ir jāpiemēro KVL
-8+1i+3i = 0
4i = 8 => I = 8/4
I = 2A
ΔR = 5Ω – 3Ω
ΔR = 2Ω
Kompensācijas spriegums ir
Vc = I [ΔR]
Vc = 2 × 2
Vc = 4 V
Kompensācijas teorēma maiņstrāvas ķēdēs
Atrodiet strāvas plūsmas izmaiņas šādā maiņstrāvas ķēdē, ja 3 omu rezistors tiek aizstāts ar 7 omu rezistoru ar kompensācijas teorēmu, un arī pierādiet šo teorēmu.
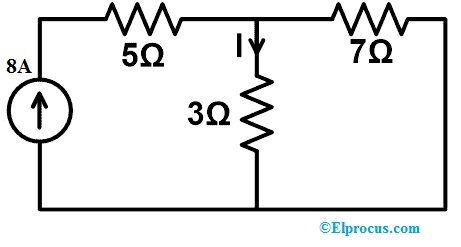
Iepriekš minētajā shēmā ir iekļauti tikai rezistori, kā arī atsevišķi strāvas avoti. Tādējādi mēs varam piemērot šo teorēmu iepriekšminētajai ķēdei. Tātad šī ķēde tiek piegādāta caur strāvas avotu. Tātad tagad mums ir jāatrod strāvas plūsma visā 3Ω rezistora atzarā ar palīdzību KVL vai KCL . Lai gan šo strāvas plūsmu var viegli atrast, izmantojot strāvas sadalītāja noteikumu.
Tātad, pamatojoties uz pašreizējo dalītāja noteikumu;
I = (8(7)/7+3) A => 56/10A => 5,6 A.
Faktiskajā ķēdē ar 3 omu rezistoru strāvas plūsma visā šajā atzarā ir 7 A. Tātad mums ir jāmaina šis 3 omu rezistors ar 7 omi. Šo izmaiņu dēļ tiks mainīta arī strāvas plūsma visā šajā atzarā. Tātad tagad mēs varam atrast šīs pašreizējās izmaiņas ar kompensācijas teorēmu.
Šim nolūkam mums ir jāizstrādā kompensācijas tīkls, noņemot visus pieejamos neatkarīgos avotus tīklā, vienkārši atverot strāvas avotu un īssavienojot sprieguma avotu. Šajā shēmā mums ir tikai viens strāvas avots, kas ir ideāls strāvas avots. Tātad mums nav jāiekļauj iekšējā pretestība. Šai ķēdei nākamā modifikācija, kas mums jādara, ir iekļaut papildu sprieguma avotu. Tātad šī sprieguma vērtība ir;
CV = I ΔZ => 7 × (7–3)
CV = 7 × 4 => 28 V
Tagad zemāk ir parādīta kompensācijas ķēde ar sprieguma avotu.
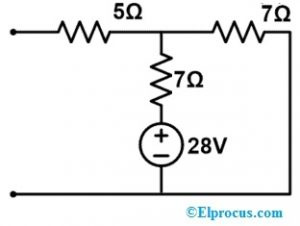
Šī ķēde ietver tikai vienu cilpu, kurā strāva tiek piegādāta visā 7Ω atzarā, nodrošinās mums strāvas izmaiņu plūsmu, t.i., (∆I).
ΔI = VC ÷ (7+7) => 28 ÷ 14 => 2 A
Lai pierādītu šo teorēmu, mums ir jāatrod strāvas plūsma ķēdē, pievienojot 7Ω rezistoru, kā parādīts zemāk esošajā shēmā.
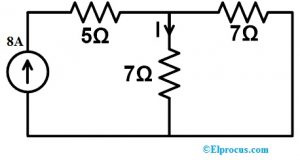
I” = (8 (7)) ÷ (7 + 7)
I” = 56 ÷ 14
I” = 4 A
Tagad izmantojiet pašreizējā dalītāja noteikumu;
Lai atrastu strāvas izmaiņas, šī strāva ir jāatņem no strāvas, kas iet caur sākotnējo tīklu.
ΔI = es – es”
ΔI = 7 – 4 => 3 A
Līdz ar to kompensācijas teorēma ir pierādīta.
Kāpēc mums ir vajadzīga kompensācijas teorēma?
- Kompensācijas teorēma ir ļoti noderīga, jo tā sniedz informāciju par izmaiņām tīklā. Šī tīkla teorēma arī ļauj mums noskaidrot precīzas pašreizējās vērtības jebkurā tīkla atzarā, tiklīdz tīkls ir tieši aizstāts ar jebkādām konkrētām izmaiņām vienā solī.
- Izmantojot šo teorēmu, mēs varam iegūt aptuveno minimālo izmaiņu efektu tīkla elementos.
Priekšrocības
The kompensācijas teorēmas priekšrocības iekļaujiet tālāk norādīto.
- Kompensācijas teorēma sniedz informāciju par izmaiņām tīklā.
- Šī teorēma darbojas uz Ohma likuma pamatjēdziena.
- Tas palīdz atklāt sprieguma vai strāvas izmaiņas, kad ķēdē ir pielāgota pretestības vērtība.
Lietojumprogrammas
The kompensācijas teorēmas pielietojumi iekļaujiet tālāk norādīto.
- Šo teorēmu bieži izmanto, lai iegūtu aptuveno mazo izmaiņu efektu elektrotīkla elementos.
- Tas ir ļoti noderīgi, jo īpaši, lai analizētu tiltu tīkla jutīgumu.
- Šī teorēma tiek izmantota, lai analizētu tīklus, kuros tiek mainītas zaru elementu vērtības, kā arī lai pētītu tolerances ietekmi uz šādām vērtībām.
- Tas ļauj noteikt pareizās strāvas vērtības jebkurā tīkla filiālē, tiklīdz tīkls ir tieši aizstāts ar jebkādām konkrētām izmaiņām vienā darbībā.
- Šī teorēma ir nozīmīgākā tīkla analīzes teorēma, kas tiek izmantota elektrotīkla jutīguma aprēķināšanai un elektrisko tīklu un tiltu risināšanai.
Tādējādi šis ir kompensācijas pārskats teorēma tīkla analīzē – problēmu piemēri un to pielietojumi. Tātad šajā tīkla teorēmā pretestību jebkurā ķēdē var mainīt ar sprieguma avotu, kam ir līdzīgs spriegums, kad spriegums krītas pāri mainītajai pretestībai. Šeit ir jautājums jums, kas ir superpozīcijas teorēma ?